Electronic properties of 2D and 1D systems

Prev:LabQSM#Module 3: Low dimensional structures (6h)

• 
  Graphene sheet: Picture by AlexanderAlUS]
• 
  Rolling graphene sheets: Carbon Nanotubes

Input set-up for a low dimensional system:

Now we want to deal with systems of reduced dimensionality, e.g. periodic in one or two dimension but isolated in the other directions. This is accomplished by:

• Isolating the system in the non-periodic dimension as seen in Electronic properties of isolated molecules, so inserting an amount of vacuum in the supercell.
• Sampling the Brillouin zone that now has reduced dimension:

In Quantum ESPRESSO one needs to set the following:

  K_POINTS automatic
  nk nk 1   0 0 0     

this will generate a 2D sampling. In brief: you will need large supercells because of the present of vacuum which reflects in a large number of plane waves and a converged sampling of the BZ. The combination of this two issues makes the calculations of 2D system rather cumbersome.

Exercises:

Exercise 1: Graphene

Honeycomb lattice structure of graphene.Picture from: J. Fuchs and M. Goerbig: Introduction to the Physical Properties of Graphene

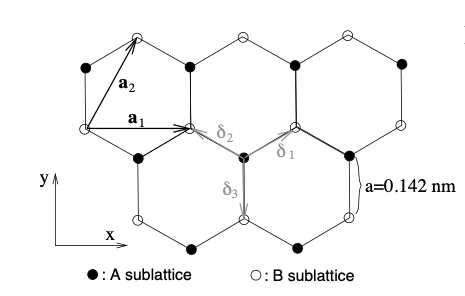
• build a supercell for an ideal graphene structure
• relax the supercell
• calculate the graphene band structure
• calculate the density of states projected on π and σ states

Hints

Exercise 2: 2D Hexagonal Boron Nitride (hBN)

Hexagonal Boron Nitride sheet

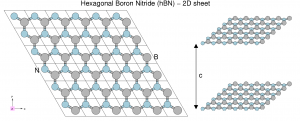
• build a supercell for 2D hBN
• calculate the DOS and band structure
• Calculate the electronic structure for bulk hBN, what is the main difference wrt the 2D structure?

Hints

Exercise 3: A small Carbon nanotube (CNT)

Memo

• Picture of the rolling sheet
• Picture of the Dirac cone slice
• Link to the tube generator