Structural and electronic properties of semiconductors and metals
Prev: LabQSM#Lecture 1: Basic DFT calculations and Convergences
Structural and electronic properties of Diamond

In this tutorial we will see how to setup a calculation and to get total energies using the PW code from the Quantum ESPRESSO distribution.
Some helpful conversions:
1 bohr = 1 a.u. (atomic unit) = 0.529177249 angstroms.
1 Rydberg = 13.6056981 eV
1 eV =1.60217733 x 10-19 Joules
For all first-principles calculations, you must pay attention to two convergence parameters. The first one is the energy cutoff, which is the max kinetic energy used in wave-function expansion. The second is the number of k-points, which measures how well the continuous integral over the BZ is discretized.
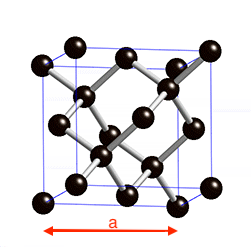
Diamond is a face-centered cubic structure with two C atoms at 0 0 0 and 0.25 0.25 0.25 a is the lattice parameter
Now let's see in detail how a QE input is structured to make a total energy calculation for this system. An example can be found in ~/LabQSM/LAB_1/test_diamond/scf.diamond.in that you can read e.g. using the editor vi:
Input file description
&CONTROL
prefix='diamond',
calculation = 'scf'
restart_mode='from_scratch',
pseudo_dir = './pseudo/'
outdir = './SCRATCH'
/
&SYSTEM
ibrav = 2,
celldm(1) = 6.7402778
nat = 2,
ntyp = 1,
ecutwfc = 40.0
/
&ELECTRONS
mixing_mode = 'plain'
mixing_beta = 0.7
conv_thr = 1.0d-8
/
ATOMIC_SPECIES
C 12.011 C.pz-vbc.UPF
ATOMIC_POSITIONS (alat)
C 0.00 0.00 0.00
C 0.25 0.25 0.25
K_POINTS {automatic}
4 4 4 0 0 0
The input file for PWscf is structured in a number of NAMELISTS and INPUT CARDS:
&NAMELIST1 ... / &NAMELIST2 ... / &NAMELIST3 ... / INPUT_CARD1 .... .... INPUT_CARD2 .... ....
The use of NAMELISTS allows to specify the value of an input variable, not all the variables need to be specified, for most variable, a default value is assigned. Variable can be inserted in any order. NAMELISTS are read in a specific order. INPUT CARDS are specific of QuantumESPRESSO codes and are used to provide input data that are always needed.
There are three mandatory NAMELISTS:
- &CONTROL: variables that control the kind of calculation (here scf), where to get the pseudopopotentials, and the verbosity needed in the output.
- &SYSTEM: variables specifying the system as the crystal structure, number of atoms, dimension of the basis set.
- &ELECTRONS variables controlling the algorithm to solve the Kohn-Sham equations.
Next, we have three mandatory INPUT CARDS:
- ATOMIC_SPECIES : name, mass and pseudopotential file
- ATOMIC_POSITIONS: atom type and coordinate in the unit cell
- K_POINTS: definition of the k point grid for the BZ integration
Other NAMELISTS relative to other kinds of calculations as relaxations, cell relaxations and other INPUT CARDS will be shown later.
The complete list of QE variables can be found in the documentation of the code at: | http://www.quantum-espresso.org/Doc/INPUT_PW.html
Now that we know how a QE input looks like let's run it and see what the code does and analyze the output:
Running pw.x
Let's create a working directory e.g.
mkdir diamond
and copy in this directory the scf.diamond.in input file we have inspected.
Now you can run the pw.x executable as:
$> pw.x < scf.diamond.in > scf.diamond.out
It is also possible to run in parallel:
$> export OMP_NUM_THREADS=2 #we use 2 threads $> pw.x < scf.diamond.in > scf.diamond.out
or
$> mpirun -np 2 pw.x < scf.diamond.in > scf.diamond.out #we use 2 processors
Several files will be generated in ./SCRATCH, most of them needed mainly for post-processing now let's have a look to the readable output (scf.diamond.out).
Output file description
We can now inspect the output (scf.diamond.in > scf.diamond.out) using vi/more/less command. We found:
A recap of the configuration that is being calculated:
bravais-lattice index = 2
lattice parameter (alat) = 6.7403 a.u.
unit-cell volume = 76.5550 (a.u.)^3
number of atoms/cell = 2
number of atomic types = 1
number of electrons = 8.00
number of Kohn-Sham states= 4
kinetic-energy cutoff = 40.0000 Ry
charge density cutoff = 160.0000 Ry
convergence threshold = 1.0E-08
mixing beta = 0.7000
Exchange-correlation= SLA PZ NOGX NOGC
Deatailed information of the unit cell:
celldm(1)= 6.740278 celldm(2)= 0.000000 celldm(3)= 0.000000 celldm(4)= 0.000000 celldm(5)= 0.000000 celldm(6)= 0.000000
crystal axes: (cart. coord. in units of alat)
a(1) = ( -0.500000 0.000000 0.500000 )
a(2) = ( 0.000000 0.500000 0.500000 )
a(3) = ( -0.500000 0.500000 0.000000 )
reciprocal axes: (cart. coord. in units 2 pi/alat)
b(1) = ( -1.000000 -1.000000 1.000000 )
b(2) = ( 1.000000 1.000000 1.000000 )
b(3) = ( -1.000000 1.000000 -1.000000 )
Information on the used pseudopotential:
PseudoPot. # 1 for C read from file:
/home/max/LabQSM/pseudo/C.pz-vbc.UPF
MD5 check sum: ab53dd623bfeb79c5a7b057bc96eae20
Pseudo is Norm-conserving, Zval = 4.0
Generated by new atomic code, or converted to UPF format
Using radial grid of 269 points, 1 beta functions with:
l(1) = 0
atomic species valence mass pseudopotential
C 4.00 12.01100 C ( 1.00)
Information on the symmetries operation detected
48 Sym. Ops., with inversion, found (24 have fractional translation)
Information on the k points used to sample the Brillouin zone and FFT gird:
number of k points= 8
cart. coord. in units 2pi/alat
k( 1) = ( 0.0000000 0.0000000 0.0000000), wk = 0.0312500
k( 2) = ( -0.2500000 0.2500000 -0.2500000), wk = 0.2500000
k( 3) = ( 0.5000000 -0.5000000 0.5000000), wk = 0.1250000
k( 4) = ( 0.0000000 0.5000000 0.0000000), wk = 0.1875000
k( 5) = ( 0.7500000 -0.2500000 0.7500000), wk = 0.7500000
k( 6) = ( 0.5000000 0.0000000 0.5000000), wk = 0.3750000
k( 7) = ( 0.0000000 -1.0000000 0.0000000), wk = 0.0937500
k( 8) = ( -0.5000000 -1.0000000 0.0000000), wk = 0.1875000
Dense grid: 2685 G-vectors FFT dimensions: ( 20, 20, 20)
Intermediate energies calculated during the scf loop
Self-consistent Calculation
iteration # 1 ecut= 40.00 Ry beta= 0.70
Davidson diagonalization with overlap
ethr = 1.00E-02, avg # of iterations = 2.0
total cpu time spent up to now is 0.2 secs
total energy = -22.67865569 Ry
Harris-Foulkes estimate = -22.74103732 Ry
estimated scf accuracy < 0.12254037 Ry
...
Near the end “hopefully” our converged results Final Eigenvalues for each k point:
End of self-consistent calculation
k = 0.0000 0.0000 0.0000 ( 331 PWs) bands (ev):
-8.0812 13.3868 13.3868 13.3868
k =-0.2500 0.2500-0.2500 ( 323 PWs) bands (ev):
-6.3642 6.7040 11.6380 11.6380
Final total energy and contribution of the various terms:
! total energy = -22.68935940 Ry
Harris-Foulkes estimate = -22.68935940 Ry
estimated scf accuracy < 1.5E-09 Ry
The total energy is the sum of the following terms:
one-electron contribution = 8.08269762 Ry
hartree contribution = 1.85703398 Ry
xc contribution = -7.05484267 Ry
ewald contribution = -25.57424832 Ry
convergence has been achieved in 6 iterations
At the end of the file, you can find info on timings spent in each part of the code (subroutines):
PWSCF : 0.13s CPU 0.32s WALL
Now we can, for instance, extract the total energy calculated at each step of the self-consistent loop:
$>grep -e "total energy" scf.diamond.out
or the accuracy reached AT each step:
$> grep -e "scf" scf.diamond.out
or we can grep both of them and put in a two-column format:
$> grep -e "total energy" -e "scf" scf.diamond.out | awk '/l e/{e=$(NF-1)}/ scf / {print e, $(NF-1)}'
-22.67865569 0.12254037
-22.68899239 0.00212159
-22.68934113 0.00007686
-22.68935832 0.00000263
-22.68935938 0.00000004
-22.68935940 1.5E-09
or we can redirect to a file to be plot
$> grep -e "total energy" -e "scf" scf.diamond.out | awk '/l e/{e=$(NF-1)}/ scf / {print e, $(NF-1)}' > diamond_scf.dat
$> gnuplot
$> plot "diamond_scf.dat"
Exercises:
Exercise 1
Convergence wrt k-points
- Using a script, perform different runs in order to converge the absolute energy of your system with respect to the k-point sampling
(keep other variables fixed).
- You can use a cutoff lower than the converged one (~40 Ry)
- Hint: Try 4x4x4, 6x6x6, 8x8x8 etc...
- Take also a look at the number of the irreducible k-points generated by the code and at the relative execution time.