Structural and electronic properties of semiconductors and metals: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
|||
| Line 2: | Line 2: | ||
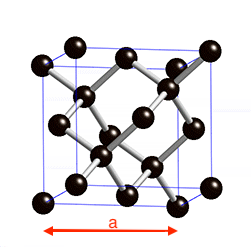
==Structural and electronic properties of Diamond == | ==Structural and electronic properties of Diamond == | ||
[[File:PastedImage0.png|left |thumb]] | |||
In this tutorial we will see how to setup a calculation and to get total energies using the PW code from the [https://www.quantum-espresso.org Quantum ESPRESSO] distribution. | In this tutorial we will see how to setup a calculation and to get total energies using the PW code from the [https://www.quantum-espresso.org Quantum ESPRESSO] distribution. | ||
| Line 15: | Line 15: | ||
For all first-principles calculations, you must pay attention to two convergence parameters. The first one is the '''energy cutoff''', which is the max kinetic energy used in wave-function expansion. The second is the '''number of k-points''', which measures how well the continuous integral over the BZ is discretized. | For all first-principles calculations, you must pay attention to two convergence parameters. The first one is the '''energy cutoff''', which is the max kinetic energy used in wave-function expansion. The second is the '''number of k-points''', which measures how well the continuous integral over the BZ is discretized. | ||
[[File:PastedImage0-2.png|thumb]] | [[File:PastedImage0-2.png|thumb]] | ||
Revision as of 11:06, 1 December 2020
Prev: LabQSM#Lecture 1: Basic DFT calculations and Convergences
Structural and electronic properties of Diamond

In this tutorial we will see how to setup a calculation and to get total energies using the PW code from the Quantum ESPRESSO distribution.
Some helpful conversions:
1 bohr = 1 a.u. (atomic unit) = 0.529177249 angstroms.
1 Rydberg = 13.6056981 eV
1 eV =1.60217733 x 10-19 Joules
For all first-principles calculations, you must pay attention to two convergence parameters. The first one is the energy cutoff, which is the max kinetic energy used in wave-function expansion. The second is the number of k-points, which measures how well the continuous integral over the BZ is discretized.