Solution LAB3 graphene
Jump to navigation
Jump to search
- Back to the previous page: Electronic properties of 2D and 1D systems#Exercise 1: Graphene
Step 1
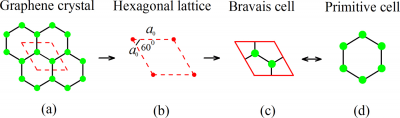
- Graphene has an honeycomb lattice and we can define the unit cell by considering an hexagonal lattice and two atoms per cell. The CC distance is 0.142nm. An input file can be set using an hexagonal bravais lattice as:
&system
ibrav= 4, celldm(1) =4.6542890, celldm(3)=something appropriate, nat= 2, ntyp= 1, [...]
/
ATOMIC_POSITIONS {crystal}
C 0.0000000 0.0000000 0.000000
C 0.3333333 0.6666666 0.000000
- Graphene is a quasi-metal, pay attention to the smearing
- K point sampling on the plane. If multiple of 3 you can include the high symmetry point K in your sampling
- You may want visualise your input using xcrysden and measure the CC distance
Step 2
- When relaxing the system you may want to keep fixed the direction orthogonal to the graphene sheet. This is done by inserting in your input the CELL namelist
&CELL cell_dofree='2Dxy' ... /
Step 3
- Let's consider the path Γ-M-K-Γ
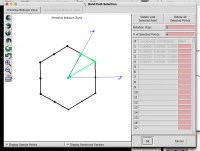
- We can get the high symmetry k-point path using xcrysden:
xcrysden --pwi scf_graphene.in
Tools->K-path selection:
Notice that the k points showed in xcrysden are in crystal_b unit.
- Perform a "bands" calculation using pw.x assigning the path e.g:
K_POINTS {crystal_b}
4
0.0 0.0 0.0 20
0.0 0.5 0.0 20
0.33333333 0.333333333 0. 20
0.0 0.0 0.0 20
- Finally we can post-process the result using bands.x
Step 4
- Calculate the electronic structure with a fine mesh of k-points (at least 48x48x1 better larger)
- Use projwfc.x to project onto the s and p orbitals. (Note the file containing the p projections show the x,y,z component in 3 columns)