Solution LAB1 ecutwfc convergence 3
- Back to the previous page: Structural and electronic properties of semiconductors and metals #Convergences
Convergence of the total energy differences and forces wrt the kinetic energy cutoff
We can use the same script as before, adding a displacement as suggested (0.05 or 0.10 alat to the component of one of the atoms in the cell).
We also want to modify the scheme for file naming (i.e. te label variable).
In practice, we can modify the script according to the following snippets:
#
# set vars
#
nk=8
alat=6.741
displ=0.01
#
ecutwfc_list="20 30 40 50 60 80 100 120 140 160 200 300 400"
[...]
label="nk${nk}_displ${displ}_ecut${ecutwfc}"
[...]
# input file
&CONTROL
[...]
tprnfor=.true.
/
[...]
ATOMIC_POSITIONS (alat)
C 0.00 0.00 0.00
C 0.25 0.25 $((0.25+$displ))
As discussed, by displacing one atom we are breaking the symmetry of the system and atomic forces different from zero can arise. This is indeed the case.
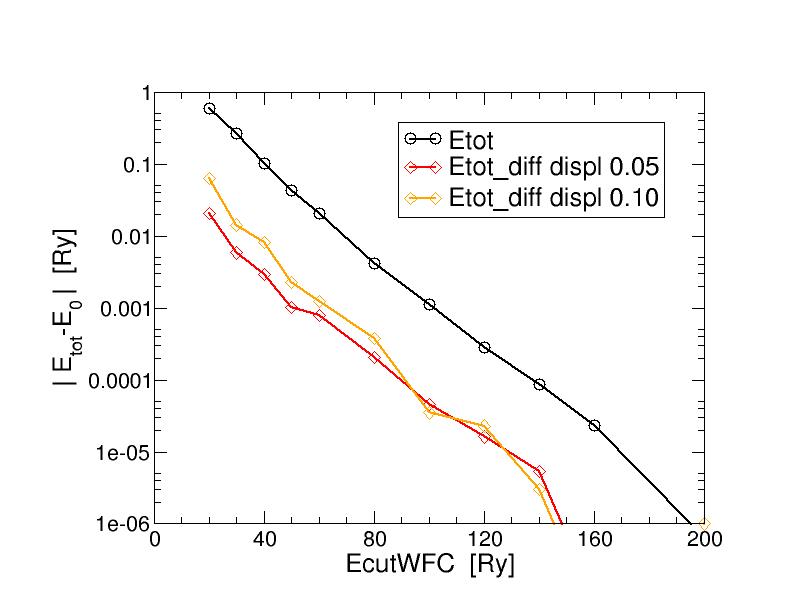
Here we can first compare the total energy differences (wrt the pristine undistorted case) as a function of kinetic energy cutoff. Plot is given in the figure:
- Comparing to the results obtained with a different lattice, here the total energy difference curves (computed with two values of the displacement) are less noisy and better behaved.
- Still, given a threshold (say 0.0001 Ry), convergence is reached significantly earlier (at about 80 Ry) than for the total energy itself.
- Different values of the displacement do not seem to have a significant impact on the final picture.
Next, we can also plot the behaviour of atomic forces wrt ecutwfc.
In order to extract data, we can look for the Force report in the output file
Forces acting on atoms (cartesian axes, Ry/au):
atom 1 type 1 force = 0.00000000 0.00000000 0.35966978
atom 2 type 1 force = 0.00000000 0.00000000 -0.35966978
Total force = 0.508650 Total SCF correction = 0.000014
and extract the <Total force> parameter. This is the norm-2 (sqrt of the sum of the components squared) of the array forces(1:3,1:natoms) containing the 3 components of the force vector for each atom.
The extract.sh script used in previous exercises can be used for the job. Here are the results:
# ecut [Ry] T.force [Ry/Bohr] 20.0000 0.683342 30.0000 0.494722 40.0000 0.525990 50.0000 0.512153 60.0000 0.510405 80.0000 0.508603 100.0000 0.508650 120.0000 0.508433 140.0000 0.508483 160.0000 0.508445 200.0000 0.508450 300.0000 0.508452 400.0000 0.508448
Again, a decent convergence is obtained for ectuwfc values of the order of 80 Ry or larger.