Solution LAB1 ecutwfc convergence
- Back to the previous page: Structural and electronic properties of semiconductors and metals #Convergences
Convergence of the total energy wrt the kinetic energy cutoff
We can start by modifying the script of the previous exercise in order to loop over different values of the
ecutwfc variable.
Note that either we do not specify ecutrho (exploiting the fact that the default value is 4*ecutwfc), or
we set it explicitly with the correct value (as the default does).
[...] # # set vars # alat=6.741 nk=8 # Here we choose a reasonable value of nk. # Since the kinetic energy cutoff is a property of the pseudopotential (transferability) # this should have no (or very little) impact. # ecutwfc_list="20 30 40 50 60 80 100 120 140 160 200"
#
# main loop
#
for ecutwfc in $ecutwfc_list ; do
#
ecutrho=$(($ecutwfc*4))
#
# here we have used the bash built-in arithmetics
# alternatively one can use e.g. awk
# ecutrho=`echo $ecutwfc | awk '{print $1*4}'`
#
label="nk${nk}_ecut${ecutwfc}"
#
filein=scf_${label}.in
fileout=scf_${label}.out
#
# generate the input file
#
cat > $filein <<EOF
&CONTROL
[...] # note here you can use shell variables
/
$SYSTEM
ecutwfc=$ecutwfc
ecutrho=$ecutrho
[...]
K-POINTS
$nk $nk $nk 0 0 0
EOF
#
# running
echo "Running $label"
#
$para_prefix $bindir/pw.x $para_postfix < $filein > $fileout
done
We can then make the script executable (if not yet) and run the calculations. As you can see, the time-to-solution of each run depends quite strongly on the chosen kinetic energy cutoff. The following considerations can be made
- for each DFT calculation, the time-to-solution (TTS) is roughly linearly proportional to the number of
used k-points.
- When we use k-grids of the kind
$nk $nk $nk 0 0 0the total number of points is proportional
to $nk^3. k-points are then reduced according to symmetry. Still, the resulting number of points
is proportional to the cube of the grid discretisation.
- Concerning the kinetic energy cutoff: the number of G-vectors is proportional to the power 3/2 of the cutoff value.
- Each scalar product of wfcs then scales linearly with the number N of G-vectors, while FFTs scale as N*logN .
- At fixed number of bands and k-points, the overall scaling of the TTS wrt ecutwfc is therefore proportional to the power 3/2
(the refactor including some logN term).
- This can be seen by plotting the TTS vs ecutwfc for the calculated data.
Data to be plotted can be extracted with a script similar to this:
$> cat extract.sh
#!/bin/bash
#
file_list=$*
output="# ecut [Ry] etot [Ry] time [sec]"
#
for file in $file_list
do
ecutwfc=`grep "kinetic-energy cutoff" $file | awk '{print $(NF-1)}'`
etot=`grep ! $file | awk '{print $(NF-1)}'`
timing=`grep "PWSCF" $file | grep "WALL" | awk '{print $(NF-3)}' | sed 's/s//'`
#
output="$output
$ecutwfc $etot $timing"
done
#
echo "$output" | sort -n
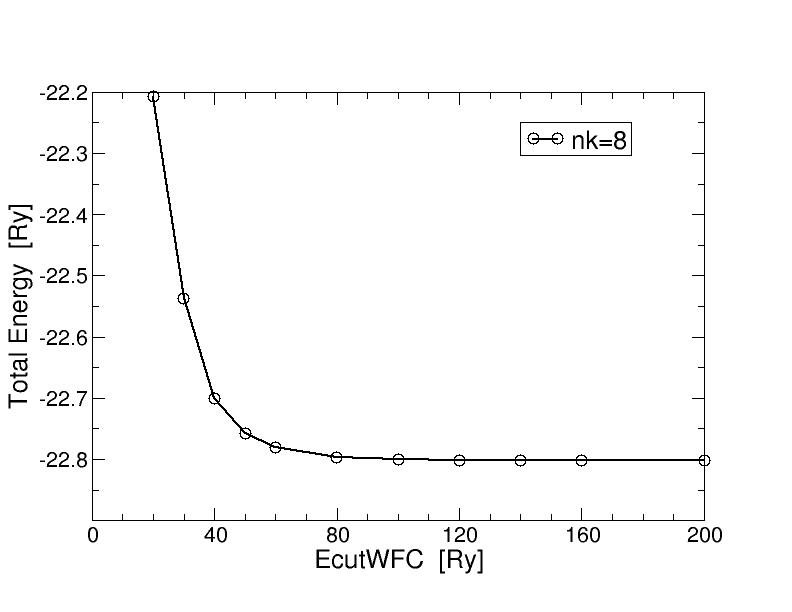
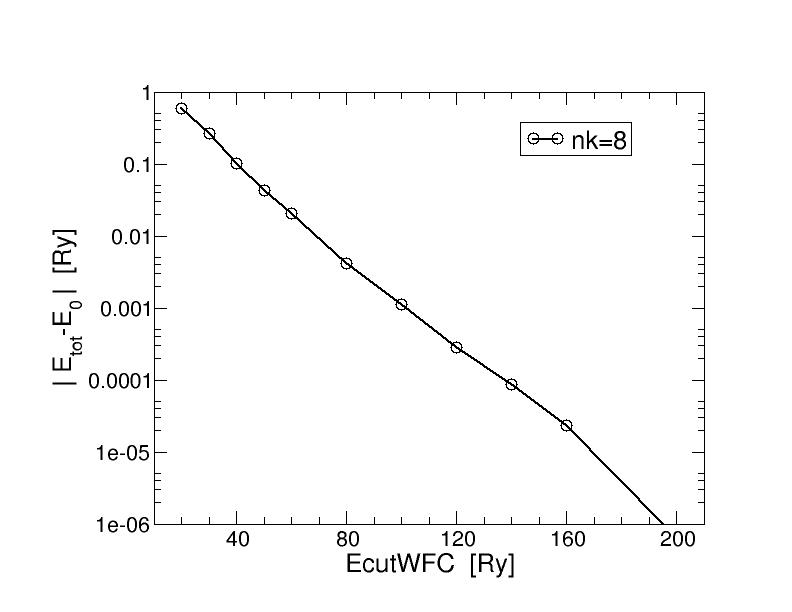
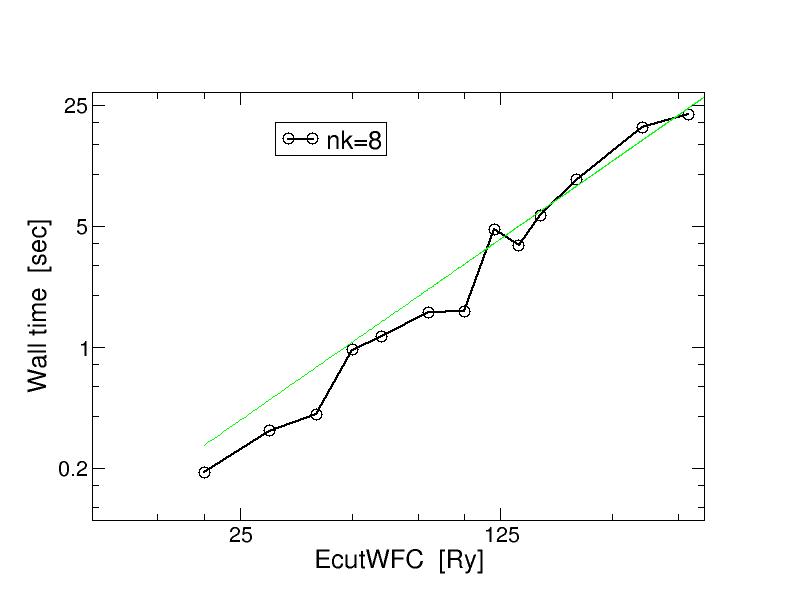
Here are the graphs showing the total energy as well as wall-time vs ecutwfc
In the total energy plot we see, especially in the one with log-scale, that requiring a convergence of 0.0001 Ry requires a kinetic energy cutoff in between 120-150 Ry (very large !!).
In the time to solution plot, in double log scale, we see that data are somehow fitted with a linear curve with slope 3/2 (-> power low with exponent 3/2).