Solution LAB1 diamond lattice parameter
- Back to the previous page: Structural and electronic properties of semiconductors and metals #Convergences
Lattice parameter of diamond
Given the convergence study of the total energy as a function of the k-point grid (as done in previous exercises), here we set the k-grid to a converged value, say
nk=8
and perform a series of total energy calculations at different lattice parameters, for several values of the kinetic energy cutoff.
Here we consider the following values:
ecutwfc_list="20 30 40 50 60 80 100 120 140 160"
for cutwfc in $ecutwfc_list
do
# run scf calculations for multiple alat values
done
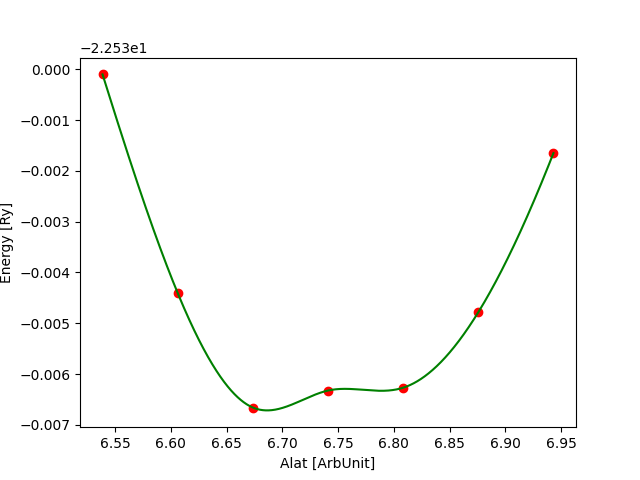
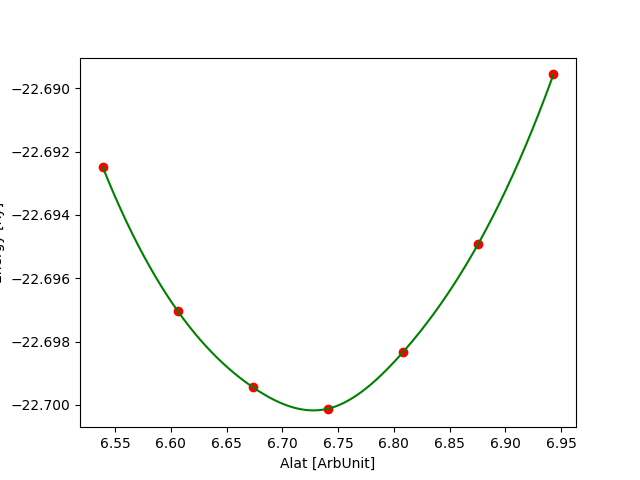
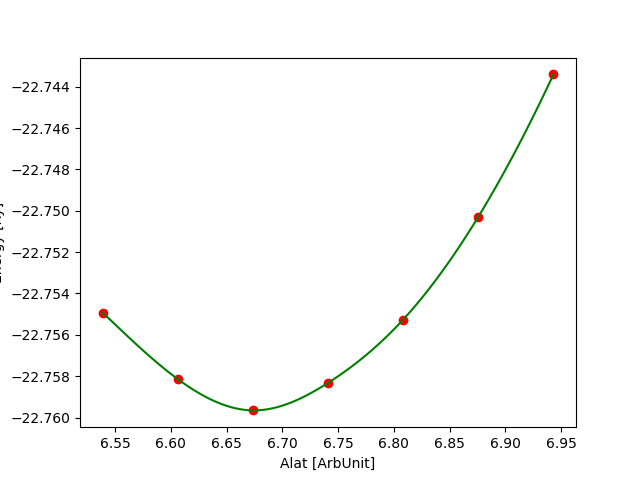
For each cutoff, Etot vs alat is fit (eg using a python script provided) and the minimum is extracted.
For instance, once data are extracted and cast in the form:
$> cat results_50Ry.dat # calculations using ecutwfc=50 Ry # alat [bohr] etot [Ry] 6.5388 -22.75492438 6.6062 -22.75814079 6.6736 -22.75965543 6.7410 -22.75832711 6.8084 -22.75526586 6.8758 -22.75029450 6.9432 -22.74340707
The script
./LabCQM/tools/analyze_lattice.py
can be used to extract the position of the minimum of the curve as well as to plot the behaviour of etot vs alat, e.g.:
./analyze_lattice.py results_50Ry.dat
The scripts developed in previous exercises can be used to run multiple calculations and to extract the data.
Results as a function of the cutoff
At first, it is important to inspect the behaviour of the total energy as a function of the lattice parameter.
Some plots for ecutwfc = 20, 30, 40 Ry and ecutwfc=50, 60, 80 Ry are reported below:
In the following you can find the fitted lattice parameter as a function of the kinetic energy cutoff used in the calculations.
# Ecut alat 20 6.8354274 30 6.686406 40 6.727857 50 6.6744762 60 6.6694212 80 6.664164 100 6.6647706 120 6.6639618 140 6.6639618 160 6.6639618
A decent convergence can be already obtained using values of the kinetic energy cutoff as low as 60-80 Ry.