Solution LAB1 bands DOS diamond
- Back to the previous page: Non self-consistent calculations: Band structures and Density Of States#Examples and Exercises
Preliminaries
Given the calculations run previously to determine the converged set of k-points, ecutwfc, and lattice parameter, here we set the following:
nk = 8 ecutwfc = 60.0 # could be lowered further alat = 6.6694212
As a preliminary step:
- make a new directory, e.g. called Diamond_BANDS
- In a situation like this it is always a good idea to start over from scratch with a fresh scf calculation.
- prepare an input file for a single scf run according to the parameters above.
&CONTROL
calculation="scf"
[...]
/
&SYSTEM
alat=...
ecutwfc=...
/
[...]
K_POINTS {automatic}
8 8 8 0 0 0
- run the calculation as:
mpirun -np 2 pw.x < scf.in > scf.out
- The use of
mpirun -np 2in the example above makes the calculation running on two MPI processes.
DOS of Diamond
We start by addressing the calculation of the DOS.
We need now to write the input file for a non-self consistent calculation using a regular k-point grid. The input file looks like:
>$ cat nscf_dos.in
&CONTROL
calculation="nscf"
verbosity="high" # not strictly needed but useful sometimes
[...]
/
&SYSTEM
alat=...
ecutwfc=...
nbnd=20 # let's include some empty states
/
[...]
K_POINTS {automatic}
20 20 20 0 0 0 # here we use a much denser kpt grid
Then we run it
mpirun -np 2 pw.x < nscf_dos.in > nscf_dos.out
Given the number of k-points requested, the calculation may take some time.
At this point we can prepare an input file for the dos.x program,
$> cat dos.in
&DOS
prefix = 'diamond'
outdir = './SCRATCH/'
degauss=0.025 ! [Ry] broadening parameter
fildos = 'dos_diamond_0.025Ry.dat'
/
The variable degauss controls the gaussian broadening used to approximate
Dirac delta's in the calculation.
Try to change this value to get a feeling of the effect is has on the computed DOS.
An example is show in the figure below.
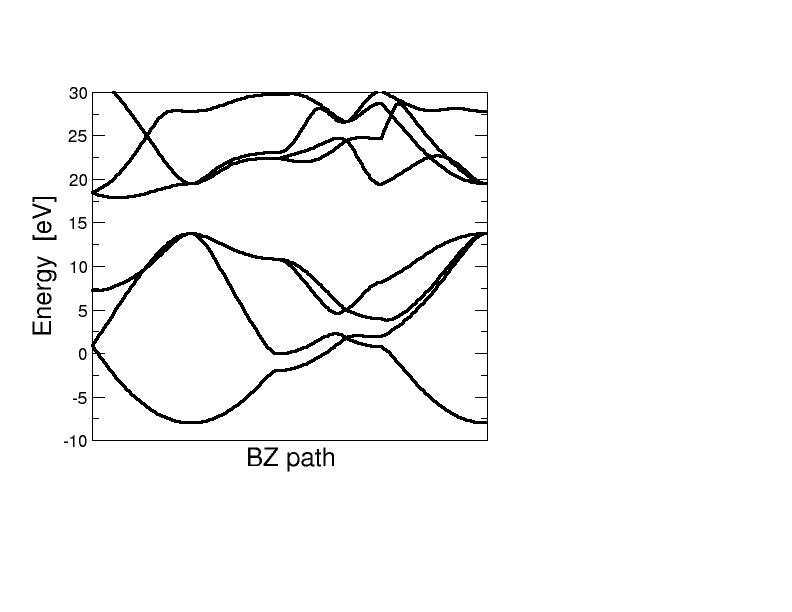
Band structure of Diamond
In order to compute a band structure we need to run a dedicated nscf calculation.
This will overwrite previous nscf calculations, but does not modify the previously compute density.
We need now to write the input file for a non-self consistent calculation using a regular k-point grid. For the sake of convenience, a plot of the zinc-blende Brillouin zone (and related conventions) is provided below.
The MaterialsCloud SeekPath tool can be also used to inspect the BZ.
The pw.x input file should look like the following:
>$ cat nscf_bands.in
&CONTROL
calculation="bands"
verbosity="high" # not strictly needed but useful sometimes
[...]
/
&SYSTEM
alat=...
ecutwfc=...
nbnd=20 # let's include some empty states
/
[...]
K_POINTS {crystal_b}
6
0.500 0.500 0.000 40 # X
0.000 0.000 0.000 40 # G
0.500 0.500 0.500 40 # L
0.750 0.500 0.250 40 # W
0.750 0.375 0.375 40 # K
0.000 0.000 0.000 1 # G
We run it as before
mpirun -np 2 pw.x < nscf_bands.in > nscf_bands.out
Next, bands can be reformatted for plotting using the bands.x provided by Quantum ESPRESSO.
Alternatively, the home-made tool
./LabQSM/tools/plot_bands.py nscf_bands.out
can be used.
The resulting plot is reported below.