Electronic properties of 2D and 1D systems
Prev:LabQSM#Module 3: Low dimensional structures (6h)
-
Graphene sheet: Picture by AlexanderAlUS
-
Rolling graphene sheets: Carbon Nanotubes
Input set-up for a low dimensional system:
Now we want to deal with systems of reduced dimensionality, e.g. periodic in one or two dimension but isolated in the other directions. This is accomplished by:
- Isolating the system in the non-periodic dimension as seen in Electronic properties of isolated molecules, so inserting an amount of vacuum in the supercell.
- Sampling the Brillouin zone that now has reduced dimension:
In Quantum ESPRESSO one needs to set the following:
K_POINTS automatic nk nk 1 0 0 0
this will generate a 2D sampling. In brief: you will need large supercells because of the present of vacuum which reflects in a large number of plane waves and a converged sampling of the BZ. The combination of this two issues makes the calculations of 2D system rather cumbersome.
Exercises:
Exercise 1: Graphene
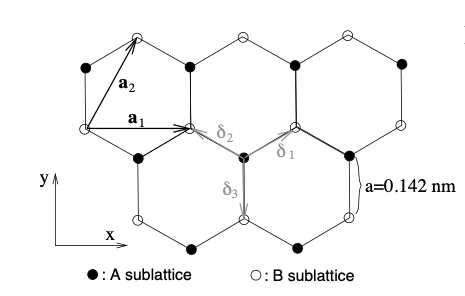
- build a supercell for an ideal graphene structure
- relax the supercell
- calculate the graphene band structure
- calculate the density of states projected on π and σ states
Exercise 2: 2D Hexagonal Boron Nitride (hBN)
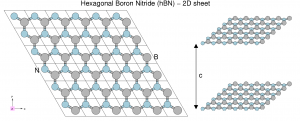
- build a supercell for 2D hBN
- calculate the DOS and band structure
- Calculate the electronic structure for bulk hBN, what is the main difference wrt the 2D structure?
Exercise 3: A small Carbon nanotube (CNT)
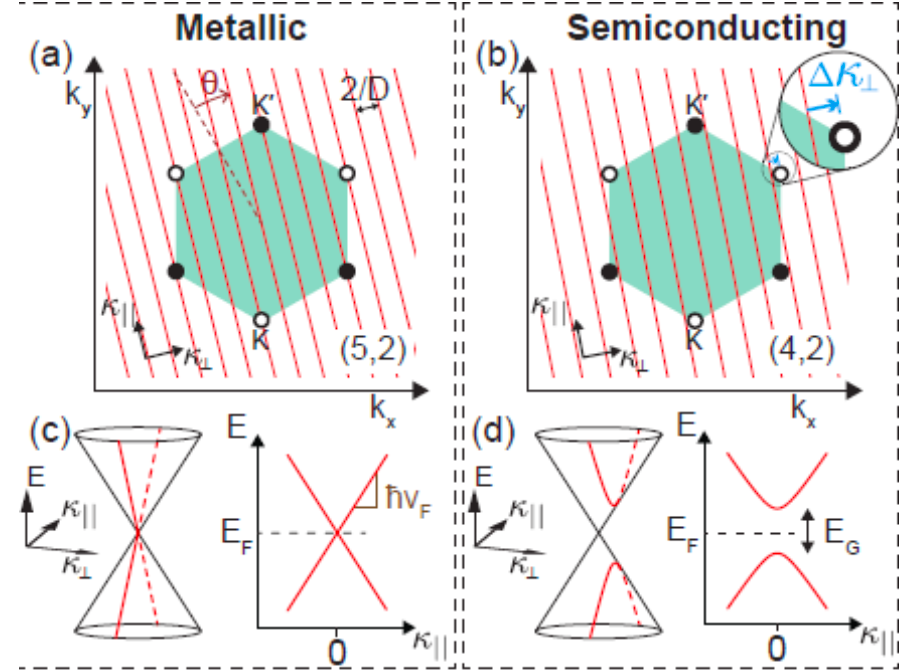
Here we want to study te electronic structure of a small carbon nanotube, obtained rolling up a graphene sheet. Interestingly the electronic structure will change drastically depending on how the rube is rolled. We can start from the graphene band structure considering the boundary condition along the circumference.
-
Sketch of Carbon nanotube band structure depending on the rolling direction
-
Carbon nanotube configurations with the chiral vector C and unit vectors a and b. From: R. Mishra et al. Textile Progress 46(2) (2014)
- Create the quantum espresso input file for the smaller CNT (3,3)
- Relax the structure
- Calculate the band structure
- Calculate the density of states (Van Hove singularity)